What is Credit Default Swap?
A Credit Default Swap (CDS) is a derivative contract between a CDS seller and a CDS buyer. CDS buyer makes periodic payments to the CDS seller till maturity. The CDS seller agrees to compensate the buyer in case of a reference entity’s credit event (like default).
In brief, a CDS transfers the credit risk of a reference entity (corporate or sovereign) from one party to another.

Finastra’s Summit is a Treasury and Capital Markets application used by major investment banks worldwide for OTC and structured products trading. Summit is a cross-asset front-to-back solution covering all aspects of a trade life cycle. Finastra Summit has deep functional capabilities in the areas of pricing, booking, risk management, back-office processing, and compliance.
Financial instruments like Bonds, Money Market instruments, FX, Swaps, Swaptions, Equity, FRA, Cap & Floor, etc., are supported by Summit for trading.
CDS is one such instrument that can also be traded using Summit.
Credit Default Swap (CDS) in Summit supports the following underlying instruments:
- SNCDS (Single Name Credit Default Swap): A Single Name Credit Default Swap (CDS) contract is an insurance contract covering the risk that a specified entity credit defaults. Following a defined credit event, the protection buyer receives a payment from the protection seller to compensate for credit losses.
- BCDS (Basket Credit Default Swap): Basket trades are based on baskets created on demand by the user. Unlike indices, each constituent in a basket may not have equal weightage. As an index, the basket trade is a single trade that represents n trades of notional x constituent weight.
- Index Credit Default Swaps: Index trades are made on standard baskets created and maintained by the International Index Company (Indexco, iTraxx) and Dow Jones (CDX). There are a variety of indices available for trading that represent different market segments and risks. Each item in an index represents a single name trade for each constituent in the index.
Mechanics of a Credit Default Swap
Figure 1: Between trade initiation and default or maturity, the protection buyer makes regular default swap payments spread to the protection seller.
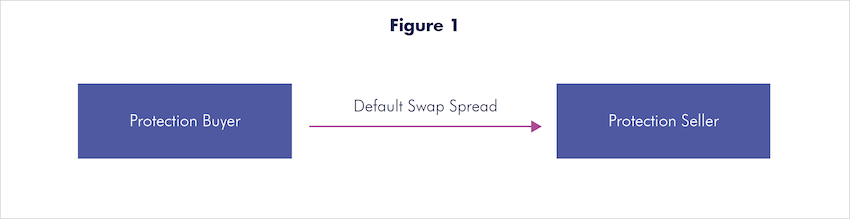
If a credit event occurs before the contract’s maturity date, there is a payment by the protection seller, known as the protection leg. This payment equals the difference between par and the price of the cheapest to deliver (CTD) asset of the reference entity on the face value of the protection and compensates the protection buyer for the loss. It can be made in cash or a physically settled format.

Example
Suppose a protection buyer purchases 5-year protection on a company at a default swap spread of 300bp. The face value of the protection is $10 million. The protection buyer therefore, makes quarterly payments approximately equal to $10 million × 0.03 × 0.25 = $75,000. Assume that after a short period, the reference entity suffers a credit event and that the CTD asset of the reference entity has a recovery price of $45 per $100 of face value.
The payments are as follows:
- The protection seller compensates the protection buyer for the loss on the face value of the asset received by the protection buyer. This is equal to $10 million × (100% – 45%) = $5.5 million.
- The protection buyer pays the accrued premium from the previous premium payment date to the time of the credit event.
For example, if the credit event occurs after a month, the protection buyer pays approximately $10 million × 0.03 × 1/12 = $18,750 of the premium accrued.
Note that this is the standard for corporate reference entity linked default swaps. For sovereign-linked default swaps, there may be no payment of premium accrued.
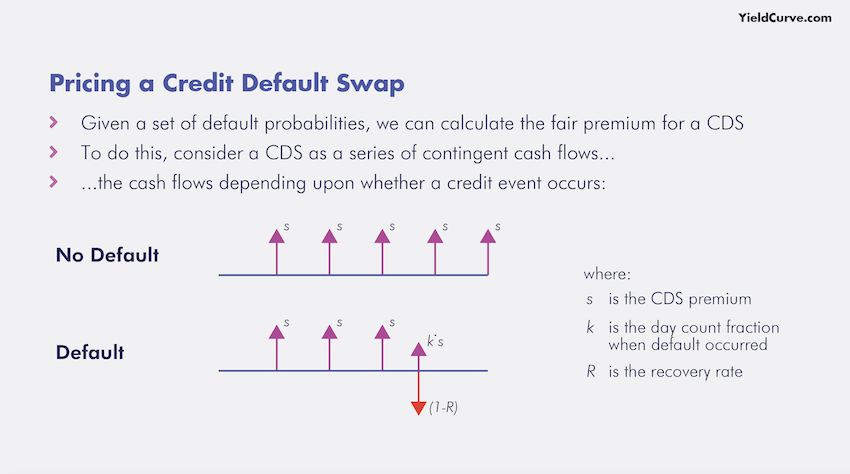
Computing The Mark-to-Market Value
Unlike bonds, the gain or loss from a CDS position cannot be computed simply by taking the difference between the current market quoted price plus the coupons received and the purchase price. We need to use a term structure of default swap spreads, a recovery rate assumption, and a model to value a CDS.
Consider an investor who initially buys 5-year protection on a company at a default swap spread of 60bp and then wishes to value the position after one year. On that date, the 4-year credit default swap spread quoted in the market was 170bp.
What is the current value of the position?
This is given by MTM = Current Market Value of Remaining 4-year Protection – Expected Present Value of 4-year Premium Leg at 60bp.
The first observation is that the investor has a CDS contract that has increased in value since he is paying only 60bp for something the market is now willing to pay 170bp. As the mark-to-market value of a new default swap is zero, this implies that the Current Market Value of the Remaining 4-year Protection = Expected Present Value of Premium Leg at 170bp.
Using this knowledge, we can state that the market-to-market value to the protection buyer is MTM = Expected Present Value of 4-year Premium Leg at 170bp – Expected Present Value of 4-year Premium Leg at 60bp.
If we define the Risky PV01 (RPV01) as the expected present value of 1bp paid on the premium leg until default or maturity, whichever is sooner, then we can restate the MTM as MTM = 170bp × Risky PV01– 60bp × Risky PV01 = 110bp × Risky PV01.
Hence, we need to calculate the Risky PV01. The Risky PV01 is called “risky” because it is the expected present value of an uncertain stream of premia. The uncertainty is that the premia payments terminate if there is a credit event.
To realize this mark-to-market gain or loss, the investor has two choices:
- Unwind it with the initial counterparty (or have it reassigned to counterparty) for cash unwind value. The cash unwind value should equal to the MTM of the position.
- Enter into the offsetting position where the investor sells protection on the same reference entity for the next four years at 170bp.
This creates a positive premium income of 170 – 60 = 110bp per annum until a credit event or maturity, whichever occurs sooner. If there is a credit event, the investor has no principal risk since the defaulted bond delivered on one side can be delivered into the protection bought, and similarly, the payments of face value are exchanged. While the investor has no principal risk, there is still a premium risk. The risk is that the reference entity does not survive until the contract’s maturity date and that the four years of 110bp of annual income are not received. These cash flows are risky, and this risk must be accounted for by the Risky PV01, which effectively discounts the cash flows at a spread over LIBOR.
Both choices have the same economic value today, but they have some differences.
In case (i) the P&L is realized immediately, and the position is terminated.
In case (ii), the P&L is only realized over the remaining life of the swap, and the investor is taking the risk that a credit event occurs and the realized P&L is less than they would have achieved if they had unwound the position for a cash amount.
On the other hand, if no credit event occurs and the net spread income is positive, they will receive more than the cash value of the unwind. This means that the financial services industry may need to adjust its asset accounts if some borrowers default on their loans during the year.
These loans are identified as “Bad Debts”, and the lender will need to mark down its assets to fair value through a contra asset such as the “allowance of bad debts”.
When the credit (lending of loan/borrowing of the loan) occurs, if the net spread income is positive, the company or the counterparty will receive the cash more than the unwind value.
CDS Trade booking in Summit
Before booking a trade in Summit, you must define the following standard static data:
- Define a Single Name Credit Entity
- Create a MUST Product to support Single Name CDS functionality
Market Data and Curve Generation for Credit Default Swaps
Data for default probabilities and recovery rates are required to price the credit derivative.
The two options to handle the probabilities include:
- Implying default probabilities directly in Summit
- Importing externally calculated default probabilities into Summit
With the first option, the default probabilities will be derived from market credit prices, which involve constructing curves using money market rates, risky bonds, and credit swap premiums. The recovery rates can also be defined as a function of time.
Once the two curves (default probability and recovery rates) are defined, invoke the curve generation functionality to imply a default probability density distribution from the market data: default curve market inputs and recovery rates. Finastra Summit uses the new market data in Summit API Toolkit functions, so clients can extend the system with their analytics, using the default probability defined in the Market Sheet. Summit supports the inclusion of externally calculated default probability data through its standard market data import program.

