1. Introduction
The purpose of this document is to analyze the performance of different candidate interpolation methods in Summit to find the best interpolation method to build a smooth USD SOFR zero curve. This is used as a benchmark for comparison purposes.
A lot of interpolation methods for curve bootstrap exist in Summit.
In this section, we will focus on studying the selected candidates bootstrapping methodologies in Summit:
- Raw and Continuous
- Raw and Hermite
- Par and Continuous
- Par and Hermite
And Bloomberg Smooth Forwards interpolation methodology will be used as the benchmark approach.
2. USD SOFR – Curve Definition
To compare apples with apples, the only variable would be the interpolation method, and the zero curve will be constructed with the same instrument. For USD SOFR, the money market 1D point, serial 1 1M-SOFR Futures Contract, Serial 1~8 3M-SOFR Futures Contract, and SOFR Swap after 2Y will be used.
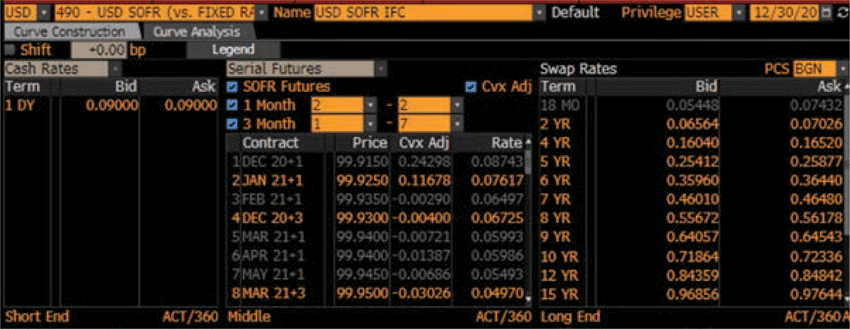
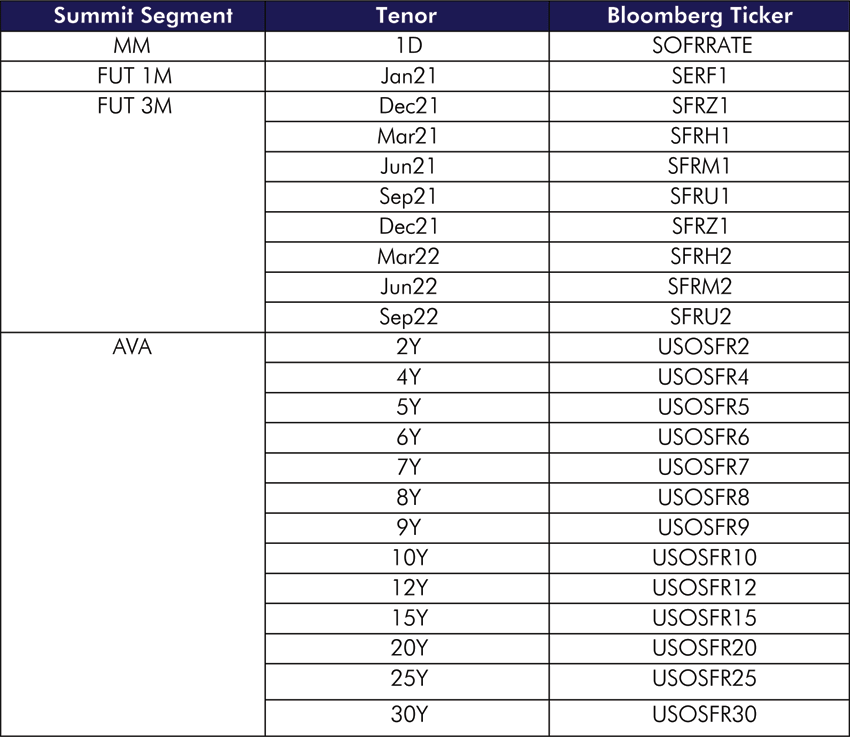
As for the comparison measurement, Hagan’s criteria and instrument recalibration will be used.
2.1 Hagan’s Criteria – Forward Curve Shape
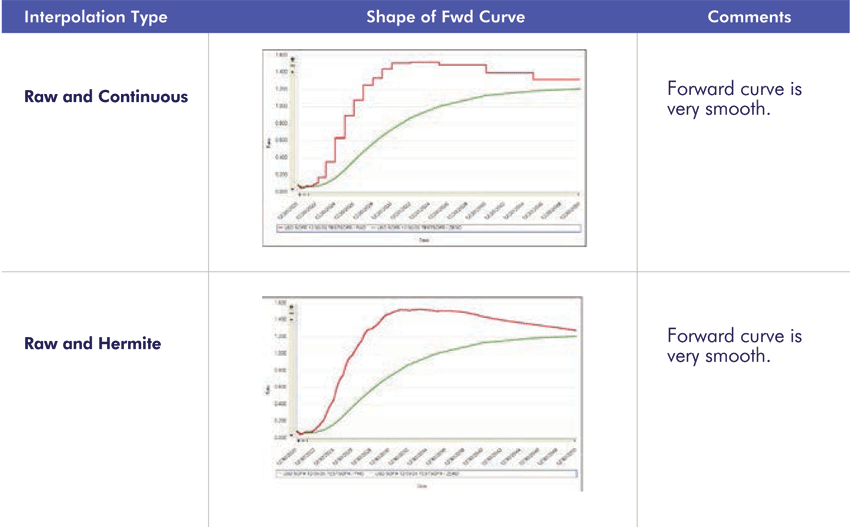
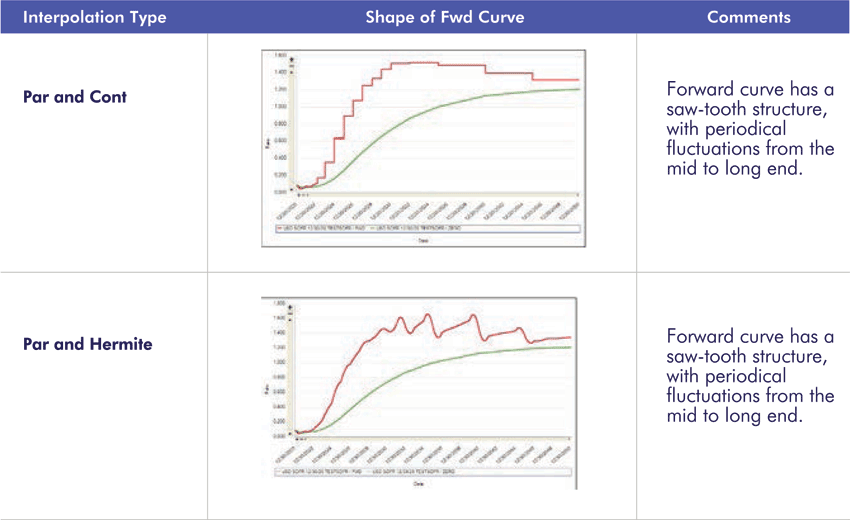
2.2 Hagan’s Criteria – Locality
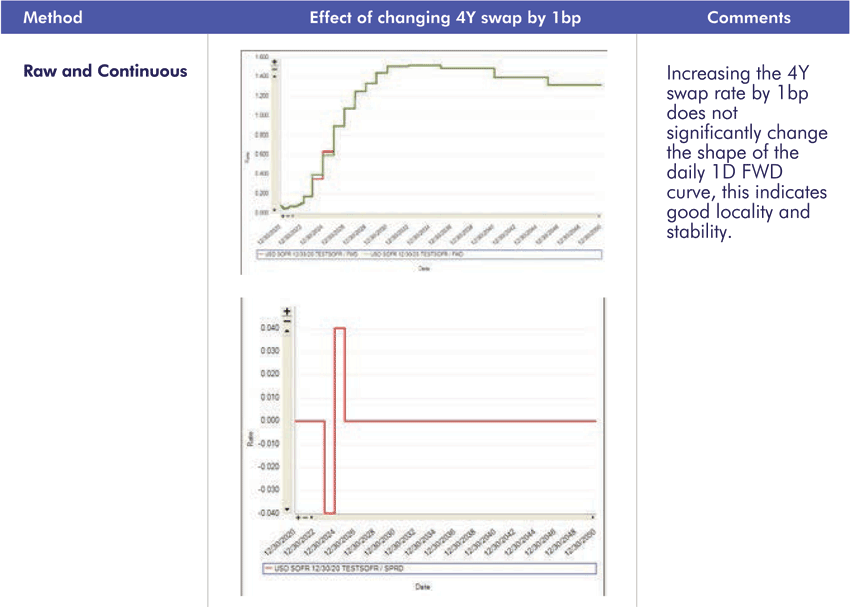
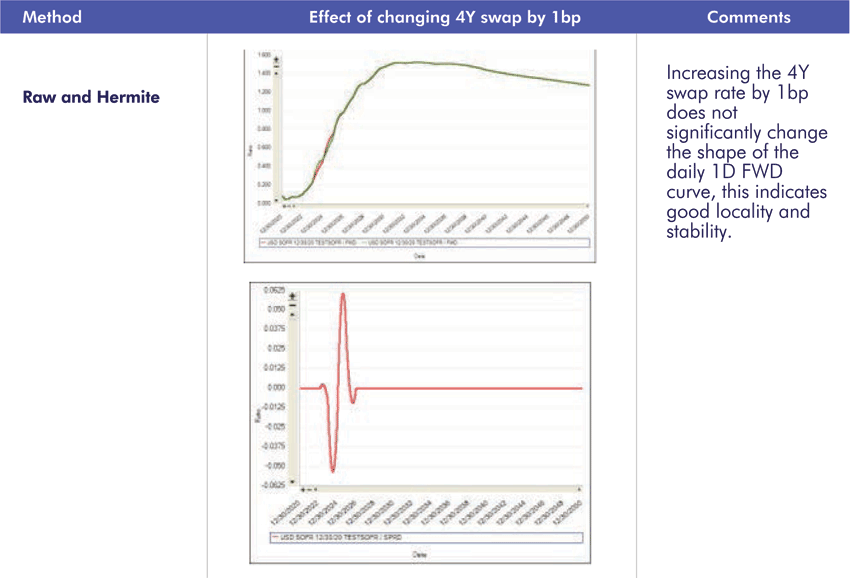
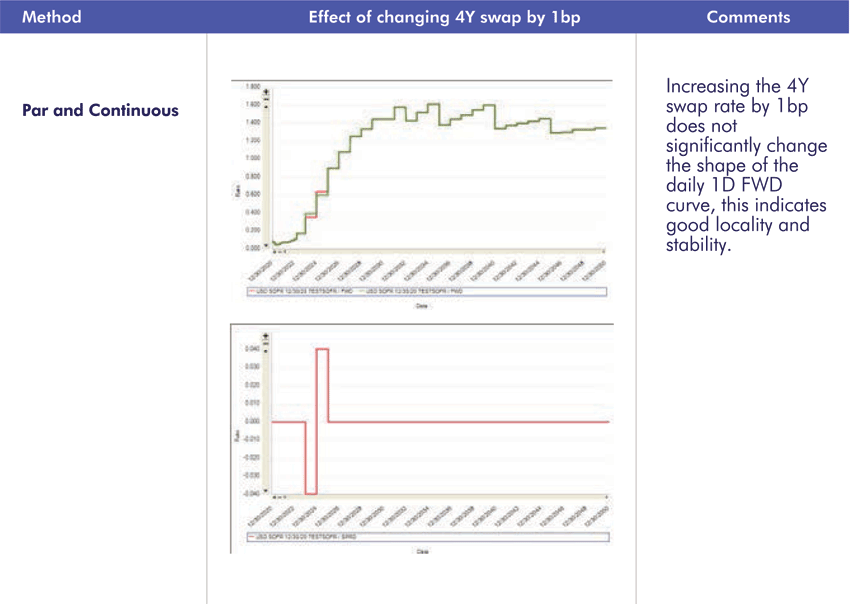
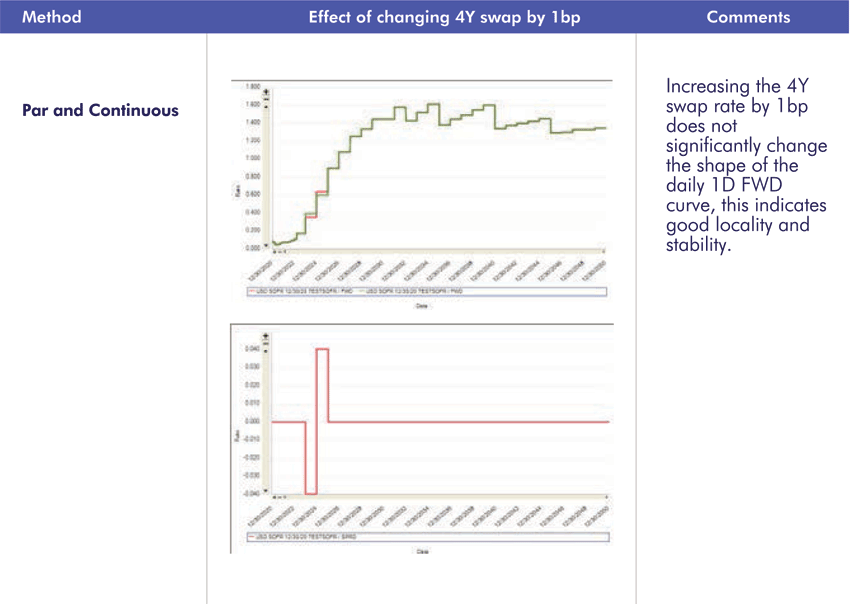
2.2 Hagan’s Criteria – Locality
Increasing the 4Y swap rate by 1bp, the maximum changes in the forward trade from the curve is as follows.

All four interpolation methodologies show good stability.
2.4 Instrument Recalibration
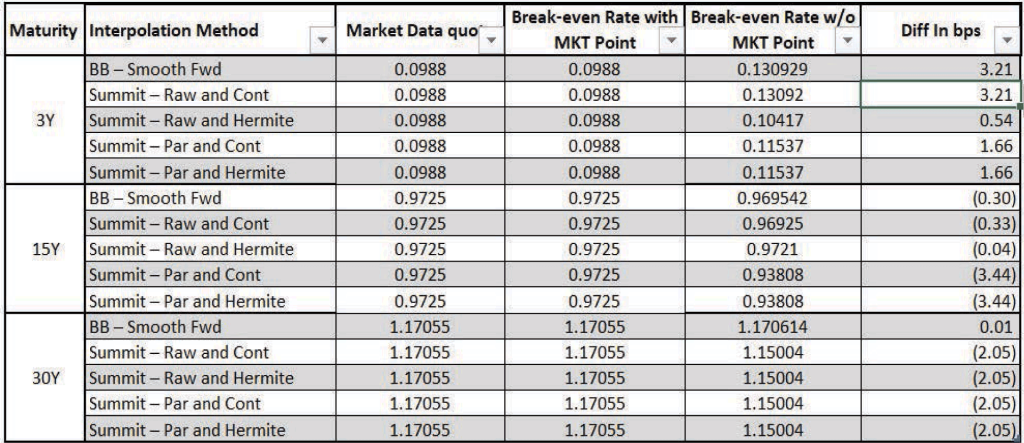
– Break-even Rate Comparison
Swap details:
Notional: 10MM.
Pay Leg: X, Annually Payment, USD SOFR Discounting.
Receive Leg: USD SOFR(Compounded), Annually Payment, USD SOFR Discounting. Solve X to price Swap at Par.
As shown in the below table, Raw and Hermite interpolation gave the best performance.
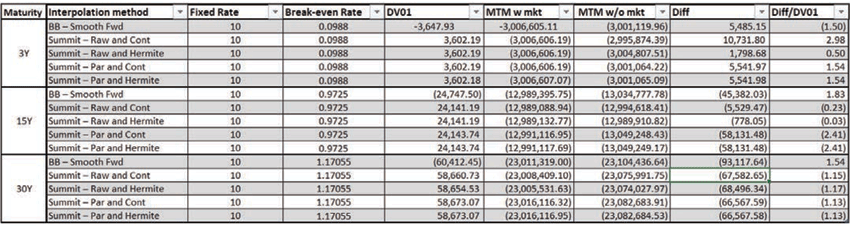
– MTM Comparison
Swap details:
Notional: 10MM.
Pay Leg: 10%, Annually Payment, USD SOFR Discounting.
Receive Leg: USD SOFR(Compounded), Annually Payment, USD SOFR Discounting.
As shown in the below table, Raw and Hermite interpolation gave the best performance.
Conclusions
Raw and Hermite is recommended for RFR Curve construction.

The choice of interpolation and bootstrap methodology is essential when building a smooth and stable zero curve in Interest Rate Curve Market Data in the Summit application.
Stay tuned for more such articles on Summit! Also, be sure to visit GreenPoint Summit for more resources on Summit!

